Resumo¶
- Cinemática: descrição das características do movimento. Observação.
- Qual a causa dos movimentos?
- Leis de Newton. Formulação de leis e teorias.
- Domínio de validade? Objetos macroscópicos e com velocidades pequenas.
Inércia¶
- Como é o movimento de um corpo livre da ação de forças e quaisquer impedimentos? Ex.: Um objeto se deslocando em um plano horizontal sem atrito.
- R.: O corpo se mantém parado, ou com velocidade constante. (Galileu. Ver Nussenzveig)
1ª Lei de Newton: na ausência de uma força resultante, a velocidade de um corpo permanecerá constante.
- Nota: pode haver forças atuando sobre a partícula. O importante é que a soma de todas as forças, $$\vec{F}_R=\vec{F_1}+\vec{F_2}+\vec{F_3}+\dots=\sum_i \vec{F_i}=\vec{0}.$$
- Nota 2: quando $\sum_i \vec{F_i}=\vec{0}$, tem-se que a partícula se move com velocidade constante. Pode-se considerar esta partícula como um referencial inercial, onde valem as leis de Newton.
- Nota 3: as leis de Newton definem os referenciais inerciais. (Tautologia)
Mudanças no movimento¶
- Como quantificar as mudanças no movimento? O movimento depende de $\vec{v}$, e mudar o movimento da partícula depende também da sua quantidade de matéria $m$.
- Ex.: Suponha que você dê um "peteleco com a mesma força" em uma bola de tênis de mesa e uma bola de boliche. É mais difícil modificar o movimento da bola de boliche, por esta possuir muito mais matéria.
Quantidade de movimento: $\vec{p}=m\vec{v}.$
- $\vec{p}$ indica o movimento de um objeto, e a sua "resistência" a mudanças no movimento (inércia).
- Sem ação de $\vec{F}$, $\vec{p}=$cte (1ª Lei). No entanto, se $\vec{F}\neq\vec{0}$, $\vec{p}$ varia.
2ª Lei de Newton: $\vec{F}=\frac{d\vec{p}}{dt}=m\frac{d\vec{v}}{dt}=m\vec{a}\text{(, se }m=\text{cte)}.$
- Nota: comportamento dinâmico partindo das $\vec{F}$'s.
- Causa das mudanças no movimento: forças!
Observações sobre a 2ª Lei de Newton¶
- Unidades de força: (massa)$\cdot$(aceleração). kg$\cdot\frac{\text{m}}{\text{s}^2}=1\text{ N}$ (SI), ou g$\cdot\frac{\text{cm}}{\text{s}^2}=1\text{ dina}$ (CGS). Conversão: $1$ dina = $10^{-5}$ N.
- $\left|\vec{F}\right|=1$ N atuando sobre uma massa de $1$ Kg produz uma aceleração de $1$ m/s$^2$, ou varia $\left|\vec{v}\right|$ desta massa em $1$ m/s a cada segundo.
- Observar que $\vec{F}_R=\frac{d\vec{p}}{dt}=m\frac{d\vec{v}}{dt}=m\vec{a}$ é uma **Eq. vetorial**, e equivale à dizer que $$\begin{cases}F_{R,x} = F_{1,x}+F_{2,x}+F_{3,x}+\dots = \sum_i F_{i,x} = m a_x,\\F_{R,y} = F_{1,y}+F_{2,y}+F_{3,y}+\dots= \sum_i F_{i,y}= m a_y,\\F_{R,z} = F_{1,z}+F_{2,z}+F_{3,z}+\dots = \sum_i F_{i,z}= m a_z.\\ \end{cases}$$
- Quando a massa da partícula varia, deve-se usar $\vec{F}=\frac{d\vec{p}}{dt}$. Ex.: Foguetes.
Referenciais inerciais¶
- As leis de Newton só valem em referenciais inerciais
- Aproximação muito boa: referencial fixo em relação às estrelas distantes, ou movendo-se com velocidade constante.
Exemplo de movimento não inercial: ônibus em movimento

Supondo um passageiro $P$ em repouso em relação à um ônibus que se move com velocidade constante. Qual é a relação entre as leis de Newton entre um observador sentado no ônibus e outro sentado na calçada? O que ocorre caso o ônibus freie rapidamente? Assuma que $P$ não possui atrito com o ônibus.
Interação entre 2 corpos¶
- Supor 2 corpos em contato, realizando forças mutuamente.
- Se o contato de $1$ com $2$ está associado à força $\vec{F}_{12}$ sobre $1$, o contato também deve produzir uma força sobre $2$, $\vec{F}_{21}$. Qual a relação entre $\vec{F}_{12}$ e $\vec{F}_{21}$?
- A única diferença possível é no sentido!
- $\vec{F}_{12} = - \vec{F}_{21}$, $|\vec{F}_{12}|=|\vec{F}_{21}|$.
3ª Lei de Newton: Para cada ação existe uma reação de mesma magnitude e direção, porém com sentido oposto.
Exemplo: Satélite em órbita¶
- $\vec{F}_{ST}$: Força exercida pela terra no satélite (força peso)
- $\vec{F}_{TS}$: Força exercida pelo satélite sobre a terra (força peso)
- $\vec{F}_{ST}=-\vec{F}_{TS}$: Par ação e reação
- Por quê a Terra "não se move"? $m_\text{Terra}\gg m_\text{satélite}$
ax = plt.axes()
# Orbita
theta = linspace(0,2*pi,100)
radius = 1
theta0 = 0.5
x = radius*cos(theta+theta0)
y = radius*sin(theta+theta0)
plot(x,y, 'k:')
# Terra
xt = 0.5*radius*cos(theta/2)
yt = 0.5*radius*sin(theta/2)
fill_between(xt,-yt,yt)
text(-0.2,-0.2,"Terra")
plot([x[0]], [y[0]], 'ro')
# Vetores velocidade
v = vector2D(origin=[x[0],y[0]], label=r'$\vec{v}$', mpl_options=uvector_style)
v.polar = (0.5, theta0+pi/2)
v.plot(ax); v.plot_label(ax, distance=-0.0)
# Vetores de força
fts = vector2D(dxdy=[0.3*x[0],0.3*y[0]], label=r'$\vec{F}_{TS}$')
fts.plot(ax); fts.plot_label(ax, distance=0.15)
fst = vector2D(origin=[x[0],y[0]], dxdy=[-0.3*x[0],-0.3*y[0]], label=r'$\vec{F}_{ST}$')
fst.plot(ax); fst.plot_label(ax, relative_position=1, distance=0.2)
axis('off')
ax.set_aspect('equal')
Alguns tipos de forças¶
Força gravitacional (próx. à superfície de planetas)¶
- Proposição: 2 massas quaisquer se atraem (Newton, 1687).
- Observável em laboratório (Cavendish, 1798).
- Em especial, a terra atrai massas próximas à sua superfície.
- $\vec{F}_g=m\vec{g}=m(-g\hat{j})\approx\vec{\text{cte}}$ próximo da superfície terrestre.
- $\vec{F}_g\equiv\vec{P}$, ou força peso.
from IPython.display import Image
torsion_pendulum = r"https://upload.wikimedia.org/wikipedia/commons/9/91/Cavendish_Torsion_Balance_Diagram.svg"
Image(url=torsion_pendulum, width=300)
Peso¶
- $|\vec{F}_g|=|\vec{P}|=P=\text{Peso}$: Magnitude da força necessária para equilibrar atração gravitacional.
- $P$ é uma força, e não massa!
- Ex.: em $P=mg$, $P$ muda sempre que $g$ varia (p.ex., devido a altitude), mesmo que a quantidade de matéria $m$ permaneça constante.
- Pergunta: qual é o peso de um astronauta?
- R.: $P$ é apenas cerca de 10% menor que seu valor na terra. $P>0$! E a micro-gravidade? Referencial acelerado!
- $P$ sempre deve ser medido em um referencial não acelerado.
Força normal $\vec{N}$¶
- Força de contato entre superfície e objeto. Sempre perpendicular à superfície.
- 'Normal' vem de 'vetor normal', ou perpendicular à superfície (matemática).
- Ex.: Objeto sobre plano horizontal, ou sobre plano inclinado.
subplot(121)
ax = plt.gca(); ax.set_aspect('equal')
axis("off")
# Desenhar um quadrado
side = 2 # lados do quadrado
c1 = vector2D(dxdy=(side,0))
c2 = vector2D(origin=c1.origin, dxdy=(0,side))
c3 = vector2D(origin=c2.tip, dxdy=c1.dxdy)
c4 = vector2D(origin=c1.origin, dxdy=c1.dxdy)
fill_between_vector2D([c1,c2,c3,c4], color="green", alpha=0.5)
# Desenhar vetores normal e peso
square_center = c1.origin + (c1.dxdy+c2.dxdy)/2
offset = array([0, 0.3])
peso = vector2D(origin=square_center-offset, dxdy=(0, -2), label=r"$\vec{P}$")
peso.plot(ax); peso.plot_label(ax, relative_position=0.6, distance=0.2)
normal = vector2D(origin=square_center+offset, dxdy=(0, 2), label=r"$\vec{N}$")
normal.plot(ax); normal.plot_label(ax, relative_position=0.2, distance=-0.2)
ylim(-2,4)
subplot(122)
ax = plt.gca(); ax.set_aspect('equal')
axis("off")
# Desenhar um plano inclinado
tside = 10
v1 = vector2D(dxdy=(tside,0))
v2 = vector2D(origin=v1.origin, dxdy=(0,0.5*tside))
v3 = vector2D(origin=v2.tip, dxdy=v1.dxdy-v2.dxdy)
fill_between_vector2D([v1,v2,v3], color="brown", alpha=0.5)
# Desenhar o ângulo theta
vc1 = vector2D(origin = v3.tip, dxdy=-v3.dxdy)
vc2 = vector2D(origin = v1.tip, dxdy=-v1.dxdy)
vc2.plot_angle(ax, vc1.polar[1], length=5, distance=-2, label=r"$\theta$")
# Desenhar um quadrado sobre o plano inclinado
side = 2 # lados do quadrado
ll_corner = v2.tip + 0.4*(v1.dxdy-v2.dxdy) # quina inferior esquerda
c1 = vector2D(origin = ll_corner, dxdy=(side,0))
c1.polar = (c1.polar[0], v3.polar[1])
c2 = vector2D(origin=c1.origin, dxdy=(0,side))
c2.polar = (c2.polar[0], c2.polar[1]+v3.polar[1])
c3 = vector2D(origin=c2.tip, dxdy=c1.dxdy)
c4 = vector2D(origin=c1.origin, dxdy=c1.dxdy)
fill_between_vector2D([c1,c2,c3,c4], color="green", alpha=0.5)
# Desenhar vetores normal e peso
square_center = c1.origin + (c1.dxdy+c2.dxdy)/2
peso = vector2D(origin=square_center, dxdy=(0, -3), label=r"$\vec{P}$")
peso.plot(ax); peso.plot_label(ax, relative_position=0.6, distance=0.2)
normal = vector2D(origin=square_center, dxdy=(0, 1.5), label=r"$\vec{N}$")
normal.polar = (normal.polar[0], normal.polar[1]+v3.polar[1])
normal.plot(ax); normal.plot_label(ax, relative_position=0.2, distance=-0.2)
- Ex.: Qual a Força Normal sobre uma pessoa num elevador nas situações 1 e 2?
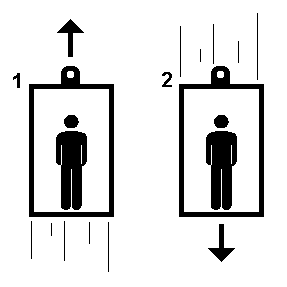
- 1) $N-P = ma > 0$, ou $N>P$
- 2) $N-P = ma < 0$, ou $N < P$
- O que acontece quando $a=-g$?
Força de atrito $\vec{F}_{at}$¶
- Resistência ao movimento paralelo da superfície devido às forças de contato.
- Relacionado com $\vec{N}$. Ex.: se $N=0$, então $F_{at}=0$. Mais detalhes adiante...
- Ex.: plano inclinado.
ax = plt.gca(); ax.set_aspect('equal')
axis("off")
# Desenhar um plano inclinado
tside = 10
v1 = vector2D(dxdy=(tside,0))
v2 = vector2D(origin=v1.origin, dxdy=(0,0.5*tside))
v3 = vector2D(origin=v2.tip, dxdy=v1.dxdy-v2.dxdy)
fill_between_vector2D([v1,v2,v3], color="brown", alpha=0.5)
# Desenhar o ângulo theta
vc1 = vector2D(origin = v3.tip, dxdy=-v3.dxdy)
vc2 = vector2D(origin = v1.tip, dxdy=-v1.dxdy)
vc2.plot_angle(ax, vc1.polar[1], length=5, distance=-2, label=r"$\theta$")
# Desenhar um quadrado sobre o plano inclinado
side = 2 # lados do quadrado
ll_corner = v2.tip + 0.4*(v1.dxdy-v2.dxdy) # quina inferior esquerda
c1 = vector2D(origin = ll_corner, dxdy=(side,0))
c1.polar = (c1.polar[0], v3.polar[1])
c2 = vector2D(origin=c1.origin, dxdy=(0,side))
c2.polar = (c2.polar[0], c2.polar[1]+v3.polar[1])
c3 = vector2D(origin=c2.tip, dxdy=c1.dxdy)
c4 = vector2D(origin=c1.origin, dxdy=c1.dxdy)
fill_between_vector2D([c1,c2,c3,c4], color="green", alpha=0.5)
# Desenhar vetores normal e peso
square_center = c1.origin + (c1.dxdy+c2.dxdy)/2
peso = vector2D(origin=square_center, dxdy=(0, -3), label=r"$\vec{P}$")
peso.plot(ax); peso.plot_label(ax, relative_position=0.6, distance=0.2)
normal = vector2D(origin=square_center, dxdy=(0, 1.5), label=r"$\vec{N}$")
normal.polar = (normal.polar[0], normal.polar[1]+v3.polar[1])
normal.plot(ax); normal.plot_label(ax, relative_position=0.2, distance=-0.2)
fat = vector2D(origin=square_center, dxdy=(-1.0, 0), label=r"$\vec{F}_{at}$")
fat.polar = (fat.polar[0], fat.polar[1]+v3.polar[1])
fat.plot(ax); fat.plot_label(ax, relative_position=0.45, distance=0.5)
Halliday 5.55 (9ª Ed.)¶
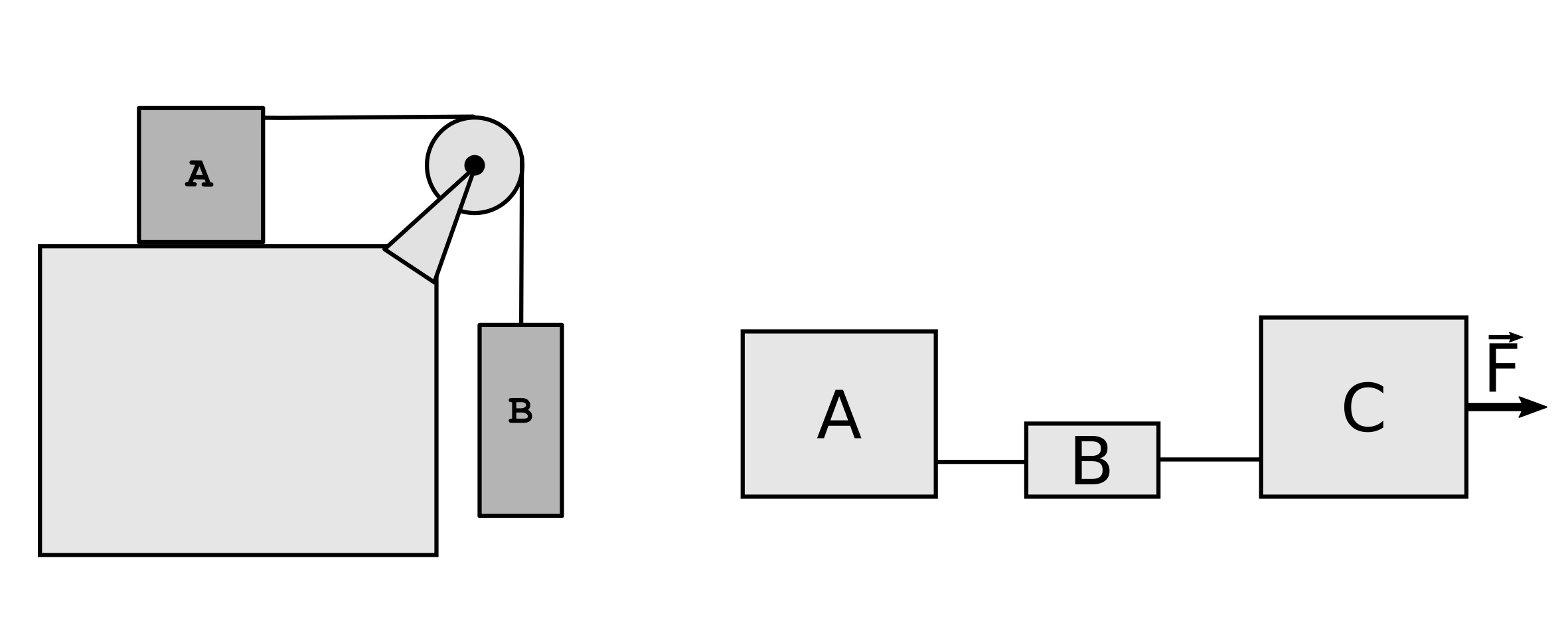
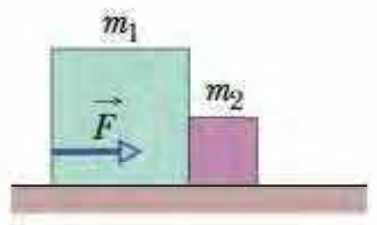
Dois blocos estão em contato em uma mesa sem atrito. Uma força horizonal é aplicada ao bloco maior, conforme a figura.
- (a) Se $m_1 = 2,3$ kg, $m_2 = 1,2$ kg e $F = 3,2$ N, determine o módulo da força entre os dois blocos.
- (b) Mostre que se uma força de mesmo módulo $F$ for aplicada ao menor dos blocos no sentido é oposto, o módulo da força entre os blocos será $2,1$ N, que não o mesmo valor calculado no item (a).
- (c) Explique a razão da diferença.
Halliday 5.57 (9ª Ed.)¶
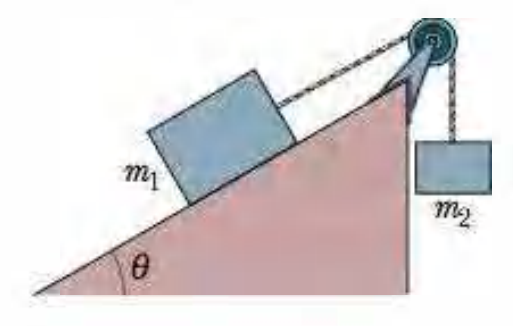
Um bloco de massa $m_1 = 3,70$ kg sobre um plano sem atrito inclinado, de ângulo $\theta = 30,0^o$, está preso por uma corda de massa desprezível, que passa por uma polia de massa e arito desprezíveis, a um outro bloco de massa $m_2 = 2,30$ kg, conforme a figura. Quais são:
- (a) o módulo da aceleração de cada bloco,
- (b) o sentido da aceleração do bloco que está pendurado, e
- (c) a tensão da corda?
Halliday 5.80 (9ª Ed.)¶
Uma pessoa de $80$ kg salta de paraquedas e experimenta uma aceleração para baixo de $2,5$ m/$s^2$. A massa do paraquedas é $5,0$ kg. Assuma $g=10$ m/s$^2$
- (a) Qual é a força para cima que o ar exerce sobre o paraquedas?
- (b) Qual é a força que a pessoa exerce sobre o paraquedas?